Spins, qubits, and the many-body problem
Going down a rabbit hole where qbits mirror NMR spins and simulate artificial molecules
As an MR engineer, it is not often that I read about quantum computers. However, an hour ago a post showed up on my Facebook feed saying that Google’s Quantum AI team used quantum echoes to predict two molecular structures that were then validated via NMR spectroscopy. They were talking about time reversal, refocusing, and decoherence, concepts that have been part of our everyday NMR vocabulary for decades.
In magnetic resonance, an echo appears when we reverse the dephasing of spins caused by field inhomogeneities. A simple 180° pulse undoes that phase dispersion, and the signal comes back refocused. Small perturbations will result in imperfect echoes but will also reflect the underlying structure that caused that perturbation. Diffusion imaging is an example of this that I use on a daily basis.
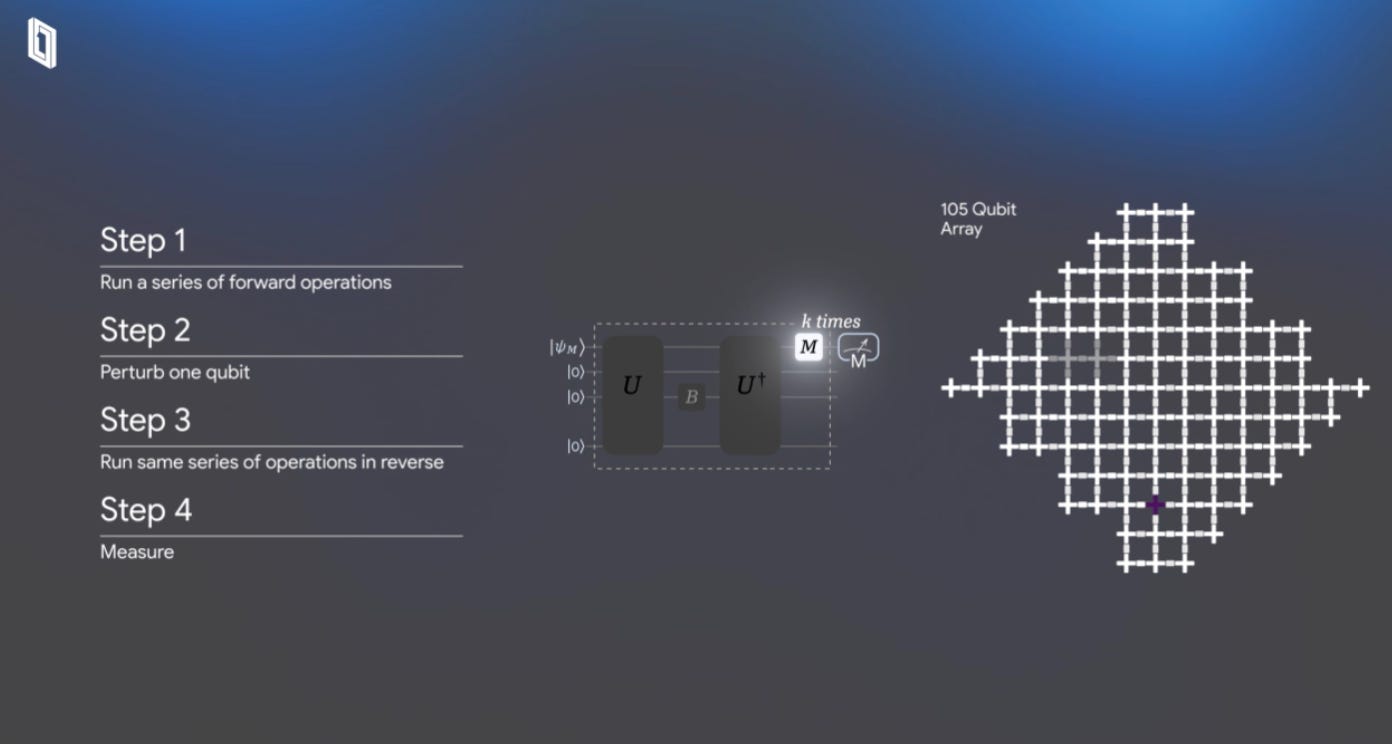
In the Quantum AI experiment the principle is the same but applied to a completely different playground. Instead of nuclear spins, they use superconducting qubits and treat them as artificial atoms that can be controlled with astonishing precision. These qubits evolve under a complex Hamiltonian, spreading quantum information throughout the system. Then, by effectively reversing that evolution, the team measures how much of the original “state” returns.
They call this a quantum echo. It’s not magnetization refocusing this time, but the reversal of information scrambling. When the echo fades, it’s not because of T₂ decay or gradient dephasing, but because quantum information has become too entangled to unscramble. This phenomenon is captured by what physicists call the “out-of-time-ordered correlator,” or OTOC.
The mathematical backbone of this experiment would look surprisingly familiar to anyone who’s ever designed a spin-echo or multiple-quantum NMR sequence. The entire idea of evolving under one Hamiltonian and then inverting it is straight out of our playbook. In fact, the authors explicitly mention that solid-state NMR spin networks inspired their approach.
The impressive part of Google’s result is the speed. Their quantum processor finished a computation in about 30 seconds, whereas a classical supercomputer would take roughly 13,000 times longer. Simulating a network of interacting spins grows exponentially harder for classical machines, but quantum processors can evolve such systems directly.
The broader implication is intriguing. If quantum computers can reproduce the kinds of spin dynamics that we’ve spent decades observing experimentally, they might eventually help us simulate systems that are too complex for classical computation: dense solids, coupled spin networks, or even biological macromolecules. It’s not that quantum computers are becoming NMR machines, but that NMR, in a way, was doing quantum computing long before the rest of the world caught on.
P.S. For further reading I recommend this Ars Technica article, and the original papers: “Observation of constructive interference at the edge of quantum ergodicity”, arXiv:2510.19751, and arXiv:2510.19550. Google also put up an accompanying blog post, and a nice short video on Twitter summarizing the link between NMR and quantum computing.